Sidebar
prostorove_zvyrazneni
Table of Contents
- nová DN hodnota je určena v závislosti na hodnotách určitého počtu okolních prvků
- využití filtrace při shlazování snímků, zvýrazňování a detekce hran, úpravy výsledků klasifikace apod.
- prostorová frekvence = relativní změny DN hodnot vůči těm okolním
- vysokofrekvenční záznam - velké rozdíly mezi DN hodnotami (komunikace, řeky, …)
- → vysokofrekvenční filtr - propouští všechny lokální extrémy
- nízkofrekvenční záznam - postupné změny (velké lesy, pole, …)
- → nízkofrekvenční filtr - vytváří zhlazený obraz
- filtrovací okno
- lichý počet řádků a sloupců
- každý pixel v něm má váhu
- pohybuje se konvolucí
- okraj okna → změnší se nebo replikuje
nízkofrekvenční filtry
- průměrový filtr
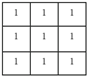
- mediánový filtr
- filtr s hodnotami vážené vzdálenosti
- jemnější zhlazení

- vážený střed
- vyšší váha → menší shlazení
- menší váha → odstranění šumu
- majoritní filtr
- modální filtr (nejčetnější hodnota)
- zachovává hodnoty
- sieve filtr
- odstraní plochy, které jsou měnší než zadaná prahová hodnota
- pixelům těchto malých ploch je přiřazena hodnota nejvyšší sousední plochy
- filtrace rotujícím oknem
vysokofrekvenční filtry
- obecně zdůrazňují objekty, které jsou menší než polovina filtrovacího okna, širší objekty potlačují → používají různé velikosti filtrů
- využití k ostření (sharpening)
- jde o zvýšení hodnot mezi centrálním pixelem a okolím
- laplaceovské filtry
- součet vah okolo, suma je 0
- nulové hodnoty pro homogenní plochy
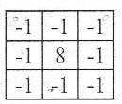
- Sobelův filtr
- zdůrazňuje vertikální nebo horizontální hrany a linie
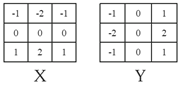
- Prewittův filtr
- podobný jak Sobelův

diferenční filtry
- vysofrekvenční informace = původní obraz - nízkofrekvenční informace (→ diferenční filtry)
- zostřující filtr
- původní obraz → průměrový filtr → odečtu ho od původního obrazu → mám linie a hrany → to přičtu k původnímu obrazu
fourierova transformace
- pomocí těchto transformací lze průběh jakékoliv jednorozměrné spojité funkce f(x), popsat pomocí série trigonometrických funkcí sinus a cosinus o různých amplitudách a frekvencích
- Fast Fourier Transformation (FFT)
- převod ze souřadného systému tvořeného jednotlivými řádky a sloupci, určitým počtem sin a cos funkcí, do frekvenčního souřadného systému
- → po této tranformaci lze snímek zobrazit ve 2D poli jako tzv. Fourierovo spektrum
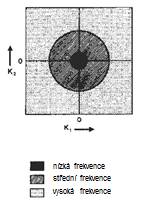
- hrany a linie orientované horizontálně v originálním obraze jsou ve Furierově spektru orientovány vertikálně a naopak; stupně šedi označují četnost výskytu dané frekvence v obraze
- frekvenční spektrum můžu pomocí inverzní FT převést zpět do prostorového souřadnicového systému a rekonstruovat tak původní obraz

- Postup:
- FFT – Fourierova transformace
- Fourierovo spektrum
- Odfiltrování vhodných frekvencí pomocí masky (černé plochy v masce indikují frekvence, které mají být potlačeny – odfiltrovány)
- Výsledný upravený obraz
Permalink prostorove_zvyrazneni.txt · Last modified: 2016/05/18 15:27 by efox
Except where otherwise noted, content on this wiki is licensed under the following license: CC Attribution-Share Alike 4.0 International
oeffentlich

